Sommario:
- Introduzione
- Una breve ripassata alla teoria
- La dichiarazione
- Funzioni di base
- Funzioni supplementari
- Alberi binari di ricerca (BST)
- Conclusioni
In questa guida voglio affrontare un argomento molto complesso e ostico: gli alberi. No, non sto parlando degli alberi quale forma di vita vegetale (quindi, voi aspiranti botanici che state leggendo, sappiate che avete sbagliato guida), ma sto parlando degli alberi quale struttura dati astratta (ADT - Abstract Data Type) utilizzata in molteplici situazioni nel campo della programmazione.
Ho voluto scrivere questa guida, in quanto non è facile trovare nel Web informazioni chiare e complete riguardanti questo argomento. Devo assolutamente precisare che con questa guida, non intendo fare una trattazione esauriente ed esaustiva dell'argomento (non basterebbe un'intera enciclopedia) ma solamente dare un valido (spero) punto di riferimento per l'implementazione e la programmazione di questa struttura e fare una panoramica veloce sulla teoria annessa. Questa guida è infatti rivolta a chi ha già nozioni sugli alberi e voglia approfondire l'aspetto della programmazione.
Inoltre, gli esempi di questa guida sono scritti (ovviamente) in C, quindi per una corretta comprensione di queste pagine, oltre a una buona conoscenza di programmazione, ricorsività e strutture dati, è utile anche una conoscenza di base di C/C++.
UNA BREVE RIPASSATA ALLA TEORIA
Un albero è un grafo orientato in cui da ogni nodo possono discendere più figli ma tale che ogni nodo, ad eccezione del nodo generatore (radice) abbia un solo padre. Un nodo è un elemento dell'albero.
Un albero, a differenza di altre s.d. (strutture dati) quali array, lista, coda, ecc., ha le seguenti caratteristiche:
- Struttura non lineare
- Struttura ricorsiva
- Struttura complessa
Il nodo da cui discende un altro nodo è detto padre. I nodi discendenti da un nodo padre sono detti figli.
Il rapporto padre-figlio dei nodi dell'albero vale per ogni nodo ad eccezione:
- della radice (ha solo figli e non ha padre)
- delle foglie (hanno solo il padre ma non hanno figli)
Una foglia, come già espresso sopra implicitamente, è un nodo terminale, ovvero un nodo senza figli. Tutti i figli di uno stesso nodo si chiamano fratelli.
Un sottoalbero è l'albero generato da un qualsiasi nodo non terminale.
Un tipo particolare di albero è l'albero binario. Un albero binario è caratterizzato dal fatto che ogni nodo può avere al massimo due figli.
Spaventati? Quanto detto fin qui vi sembra assurdo? Non allarmatevi troppo presto: lo schema in Figura 1 e quello in Figura 2 vi aiuteranno ad assimilare i concetti appena visti.
Il numero massimo di nodi di un albero binario di altezza n, è espresso dalla formula:
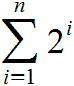
ovvero
![]()
Per visitare un albero (cioè visitarne tutti i nodi, cioè gli elementi) esistono tre modi, secondo l'ordine di visita, tutti definiti ricorsivamente.
- PREORDINE (Preorder) o ordine anticipato: R - S - D
- POSTORDINE (Postorder) o ordine posticipato o polacco: S - D - R
- INORDINE (Inorder) o ordine simmetrico: S - R - D
Dove R sta per la radice, D sta per sottoalbero destro della radice e S sta invece per sottoalbero sinistro della radice. Se non vi è chiaro questo concetto, più avanti troverete degli esempi.
Partiamo dal caso più semplice: gli alberi binari. Gli alberi binari possono essere implementati mediante record (strutture, in c) di tre campi: R (il valore del nodo, chiamato R in quanto radice del sotto albero che genera), *D (puntatore al figlio destro - e quindi al sotto albero destro generato) e *S (puntatore al figlio sinistro). Gli alberi non binari invece possono essere implementati, fra i vari modi, mediante record di due campi: la radice (o valore del nodo) e il campo che punta alla lista (o al vettore) dei figli.
In questa guida farò riferimento esclusivamente ad alberi binari in quanto gli algoritmi che agiscono su questi possono essere facilmente modificati per poter operare con alberi più complessi.
Vi ricordo inoltre che qualsiasi albero può essere ricondotto, mediante un procedimento che qui non illustrerò, ad un albero di tipo binario. Ma vediamo ora come si dichiara una struttura albero in C.
struct nodo {
// Albero di numeri interi
int DATO;
// Puntatore al sottoalbero destro
struct nodo *DX;
// Puntatore al sottoalbero sinistro
struct nodo *SX;
} NODO;
Questo è il record di tre campi di cui abbiamo parlato all'inizio: DATO, che precedentemente abbiamo chiamato R, *DX e *SX. Per chi non lo ricordasse DATO è la variabile che contiene il valore del nodo. In tutti gli esempi di questa guida supporremo che l'albero contenga valori interi. Ricordo inoltre che il C/C++ è case sensitive e che quindi "NODO" è diverso da "nodo".
Una volta dichiarata la struttura del generico nodo dell'albero, dobbiamo ora dichiarare una variabile che punti a tale struttura. Tale variabile la chiameremo tree (in inglese tree = albero):
typedef struct nodo* tree;
Questo significa che stiamo definendo un nuovo tipo di dato (typedef) di nome tree che è un puntatore a variabile di tipo nodo.
una volta dichiarato il tipo albero (in realtà abbiamo dichiarato solo un generico nodo ma, come abbiamo detto, un albero altro non è che un insieme di nodi legati in qualche modo tra loro tramite puntatori), dobbiamo ora implementare degli algoritmi che ci permettano di gestire questa struttura. Cominciamo con la costruzione di un albero binario non ordinato (vedremo in seguito cosa significa il termine "ordinato"):
tree Costruisci_Albero(int ETICHETTA,tree S,tree D)
{
tree RADICE;
// Allocazione di una nuova cella di memoria
RADICE = (nodo *) malloc(sizeof(NODO));
RADICE->DATO = ETICHETTA;
RADICE->SX = S;
RADICE->DX = D;
return (RADICE);
}
Ed ecco ora un esempio di come applicare questa funzione:
tree t1,t2;
tree t3,t4;
// Costruisce l'albero "a pezzi"
t1=Costruisci_Albero(2,Albero_Vuoto(),Albero_Vuoto());
t2=Costruisci_Albero(1,Albero_Vuoto(),Albero_Vuoto());
t3=Costruisci_Albero(7,t1,t2);
t1=Costruisci_Albero(4,Albero_Vuoto(),Albero_Vuoto());
t2=Costruisci_Albero(9,Albero_Vuoto(),Albero_Vuoto());
t4=Costruisci_Albero(3,t1,t2);
// t1 punterà all'albero appena creato
t1=Costruisci_Albero(5,t3,t4);
Questo esempio mostra come costruire un albero di radice 5 e figlio sinistro e destro rispettivamente 7 e 3 che a loro volta hanno figli sinistro e destro rispettivamente, nell'ordine, 2 1 4 9, come mostrato in Figura 3 (questo albero sarà puntato da t1). Una volta costruito l'albero vediamo ora come visitarlo. Negli esempi che seguono si stampano a video gli elementi dell'albero. Il lettore più sagace avrà già capito che la stampa e la visita di un albero sono funzioni strettamente legate tra loro poiché per stampare gli elementi di un albero bisogna contemporaneamente visitarlo. Ecco i tre tipi di visita di un albero:
void Inorder(tree RADICE)
// Funzione di visita di un'albero (qui lo si stampa)
{
if (!(Is_Empty(RADICE))) {
Inorder(Sinistro(RADICE));
// Sostituire cout con altre operazioni per altri scopi di visita
cout<<Valore_Etichetta(RADICE)<<" ";
Inorder(Destro(RADICE));
}
}
Che, stando all'esempio precedente, stamperebbe a video: 2 7 1 5 4 3 9.
void Preorder(tree RADICE)
// Funzione di visita di un'albero (qui lo si stampa)
{
if (!(Is_Empty(RADICE))) {
// Sostituire cout con altre operazioni per altri scopi di visita
cout<<Valore_Etichetta(RADICE)<<" ";
Preorder(Sinistro(RADICE));
Preorder(Destro(RADICE));
}
}
Che stamperebbe a video: 5 7 2 1 3 4 9.
void Postorder(tree RADICE)
// Funzione di visita di un'albero (qui lo si stampa)
{
if (!(Is_Empty(RADICE))) {
Postorder(Sinistro(RADICE));
Postorder(Destro(RADICE));
// Sostituire cout con altre operazioni per altri scopi di visita
cout<<Valore_Etichetta(RADICE)<<" ";
}
}
Che stamperebbe a video: 2 1 7 4 9 3 5.
Vediamo ora altre funzioni di base per operare su un albero.
tree Albero_Vuoto(void)
{
// Ritorna un albero vuoto (un puntatore NULL)
return(NULL);
}
questa funzione costruisce un albero vuoto (cioè un puntatore che non punta a niente).
int Valore_Etichetta(tree RADICE)
{
if (Is_Empty(RADICE)) abort();
// Ritorna il valore (o etichetta) del nodo
else return(RADICE->DATO);
}
Questa funzione ritorna il valore, o etichetta, della radice dell'albero passato come argomento. La funzione Is_Empty(), come vedremo tra poco, controlla prima che l'albero non sia vuoto (un albero vuoto è un albero che non esiste).
tree Sinistro(tree RADICE)
// Restituisce il sottoalbero sinistro
{
if (Is_Empty(RADICE)) return(NULL);
else return(RADICE->SX);
}
tree Destro(tree RADICE)
// Restituisce il sottoalbero destro
{
if (Is_Empty(RADICE)) return(NULL);
else return(RADICE->DX);
}
Queste due funzioni restituiscono rispettivamente il sottoalbero sinistro e destro dell'albero (o del nodo - è la stessa cosa) passato come argomento.
bool Is_Empty(tree RADICE)
{
// Questo è un confronto, non un assegnazione!
return(RADICE==NULL);
}
Come abbiamo visto prima, questa funzione ritorna un valore True se il puntatore all'albero passato come argomento è NULL, cioè se l'albero è vuoto; False in caso contrario.
bool Ricerca(tree RADICE,int X)
{
if (Is_Empty(RADICE))
return(false);
else {
if (X==Valore_Etichetta(RADICE))
return(true);
else
// Ricerca nel sottoalbero sinistro e destro
return(Ricerca(Sinistro(RADICE),X) || Ricerca(Destro(RADICE),X));
}
}
La funzione di ricerca altro non è che una modifica dell'algoritmo di visita di un albero. Questa funzione ricerca il valore X nell'albero puntato da RADICE.
Le funzioni seguenti contano rispettivamente il numero dei nodi di un albero e il numero delle foglie.
int ContaNodi(tree RADICE)
{
if(Is_Empty(RADICE)) return(0);
// Per ogni nodo visitato somma 1 alle chiamate ricorsive
else return(1 + ContaNodi(Sinistro(RADICE)) + ContaNodi(Destro(RADICE)));
}
int ContaFoglie(tree RADICE)
{
if(Is_Empty(RADICE))
return(0);
else {
if ((Sinistro(RADICE)==NULL) && (Destro(RADICE)==NULL))
return(1);
else return( ContaFoglie(Sinistro(RADICE)) + ContaFoglie(Destro(RADICE)) );
}
}
La seguente funzione determina se un albero è perfettamente bilanciato. Per la corretta definizione di albero perfettamente bilanciato fate riferimento a qualche testo di informatica oppure al disegno in Figura 4.
bool Perf_Bil(tree RADICE)
// Restituisce VERO se l'albero è perfettamente bilanciato
{
if (Is_Empty(RADICE)) return(true);
else {
if ((Sinistro(RADICE)==NULL) && (Destro(RADICE)==NULL))
// Praticamente: se il nodo è una foglia..
return(true);
else {
if ((Sinistro(RADICE)!=NULL) && (Destro(RADICE)!=NULL))
// Paraticamente: se il nodo ha tutti e due i figli..
return( Perf_Bil(Sinistro(RADICE)) && Perf_Bil(Destro(RADICE)) );
else return(false);
}
}
}
ALBERI BINARI DI RICERCA (BST)
In questi particolari tipi di alberi, chiamati anche BST (Binary Search Tree), ogni nodo dell'albero ha nel proprio sottoalbero sinistro tutti nodi con valore minore (o uguale) e nel proprio sotto albero destro, tutti nodi con valore strettamente maggiore. In poche parole sono alberi "ordinati". Un esempio di albero costruito in modo ordinato è quello della Figura 5. Vediamo ora le funzioni di creazione di un BST e di ricerca di un valore in esso.
tree Ins_Ord(int E,tree RADICE)
// Costruisce un albero binario di ricerca
{
if (Is_Empty(RADICE)) {
// Allocazione di una cella di memoria libera
RADICE=(tree)malloc(sizeof(NODO));
RADICE->DATO=E;
RADICE->SX=NULL;
RADICE->DX=NULL;
return RADICE;
}
else {
if (E<Valore_Etichetta(RADICE)) {
RADICE->SX=Ins_Ord(E,Sinistro(RADICE));
return RADICE;
}
else {
RADICE->DX=Ins_Ord(E,Destro(RADICE));
return RADICE;
}
}
}
bool RicercaBinaria(int X,tree RADICE)
// Ricerca dicotomica per alberi binari di ricerca (ordinati)
{
if (Is_Empty(RADICE)) return(false);
else {
if (X==Valore_Etichetta(RADICE)) return(true);
else {
if (X < Valore_Etichetta(RADICE))
return( RicercaBinaria(X,Sinistro(RADICE)) );
else
return( RicercaBinaria(X,Destro(RADICE)) );
}
}
}
In questo file (alberi.zip - 3k), trovate un sorgente C++ dove vengono impiegate tutte le funzioni illustrate fin qui. Per provarlo è sufficiente compilarlo ed eseguirlo con qualsiasi compilatore C standard.
Siamo così giunti alla fine di questa guida. I più attenti di voi avranno notato che non vi ho illustrato nessuna funzione che elimina un albero dalla memoria centrale (operazione fondamentale da fare al termine dell'utilizzo di questo, sia per liberare la RAM, sia per una buona tecnica di programmazione). Questo è un esercizio che vi lascio, tanto sono sicuro che chi è riuscito a seguirmi fin qui non avrà problemi a implementare da solo tale funzione (vi do un aiutino: la funzione free() vi sarà utile..).
Come ho accennato all'inizio di questa guida, sugli alberi si potrebbe parlare (quasi) all'infinito data la vastità dell'argomento. Ho preferito però, in queste pagine, circoscrivere gli argomenti trattati alla sola costruzione e gestione di un albero. In particolar modo non ho evidenziato l'utilizzo che si fa degli alberi, cioè in quali applicazioni questi vengono utilizzati (intelligenza artificiale, indicizzazione di un file, calcolo di espressioni matematiche.....). Inoltre ho preferito non trattare argomenti più complessi quali, ad esempio, il bilanciamento di un albero. Non ho avuto modo di illustrare neanche argomenti più semplici quali la modifica di un albero o la sua "linearizzazione". Per tutti questi motivi sto pensando di scrivere un'altra guida. Chissà? Appena avrò un po' di tempo forse lo farò. Per il momento accontentatevi di questa. Alla prossima.....
Questa guida ti è piaciuta o ti è stata utile? Scrivimi e dimmi cosa ne pensi. Mi incoraggerai a scriverne altre..